
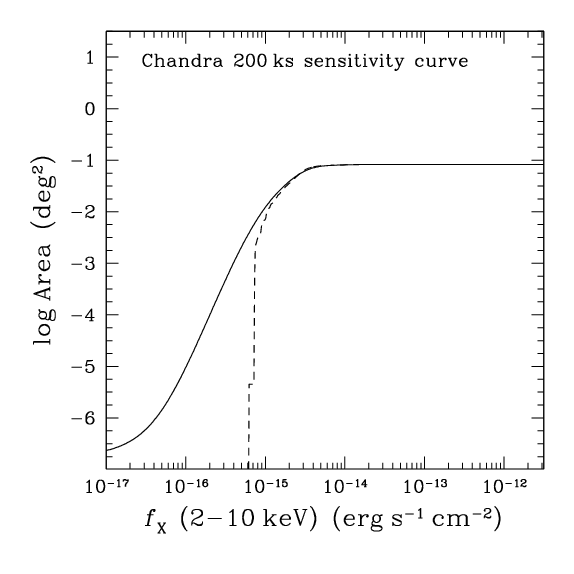
Left: Sensitivity map of a Chandra X-ray imaging observation. This is a 2-D image which provides an estimate of the probability that a source with a flux fX in a certain energy band will be detected across the detector area. The sensitivity increases from the centre of the field of view (dark) to the edge (light grey) because of instrumental effects. Our Bayesian approach for estimating the sensitivity map correctly accounts for these effects as well as biases associated with the source detection. Right: The 1-D representation of the sensitivity map is the sensitivity curve, which provides an estimate of the total detector area in which a source with flux fX can be detected. The continuous line is our new Bayesian approach, the dashed line is the standard way of estimating the sensitivity map and the sensitivity curve that does not account properly for the various sources of bias. The Bayesian sensitivity curve levels off at faint fluxes because such faint sources have a small but finite probability of producing fluctuations above the background level.